(Из австралийского журнала "AmateurRadio" за апрель 1988 г)
Lloyd Butler, VK5BR

Введение

Стоит только взглянуть на выход смесителя с помощью анализатора спектра, чтобы понять, чтосмеситель является сложным устройством. Ниже будут рассмотрены некоторые принципы смешения и смесительные устройства.

В современной аппаратуре можно обнаружить множество смесительных каскадов. Они известны как устройства, которые, при подаче на них сигналов двух частот, дают дополнительные сигналы, равные по частотам сумме и разности подаваемых на смеситель сигналов. Одна из вновь образованных компонент выделяется настроенным полосовым фильтром (резонансным контуром) и подаётся для обработки далее. Не следует забывать, что остальные компоненты, как входные, так и полученные, также, присутствуют в той или иной степени в выходном сигнале смесителя, они никуда не девались, а просто были уменьшены по амплитуде при селекции. (Следует отметить, что входные сигналы, будучи поданными на нелинейное устройство, каким является смеситель, образуют собственные гармоники, которые тоже взаимодействуют, как между собой, так и с исходными сигналами, подаваемыми на смеситель, получаемые суммарные и разностные сигналы, взаимодействуют как друг с другом, так и с исходными сигналами, их гармониками и комбинационными сигналами, полученными в результате взаимодействия уже вторичных сигналов: каждый сигнал взаимодействует с каждым, давая всё новые и новые частоты, так что на выходе нелинейного смесителя присутствует целый спектр частот с разными амплитудами, задача конструктора заключается в подавлении входных сигналов (балансное смешение по входу), двухбалансные схемы с резонансными элементами на выходе способствуют той или иной степени подавления и нежелательных выходных сигналов смесителя – UA9LAQ).

Все виды встречающихся проблем могут быть заключены в самом процессе смешения и, если Вы занимаетесь конструированием собственной аппаратуры, глубокое изучение процесса смешения Вам не помешает. Ниже делается попытка исследования основных принципов смешения.

Принципы смешения

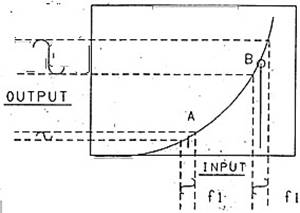
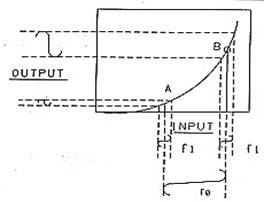
Если два сигнала с разными частотами подать на линейное устройство (например, идеальный усилитель), то они появятся на его выходе, как ни в чём не бывало, - на своих частотах. Чтобы смешать два сигнала, нам необходимо устройство с “изогнутой” или нелинейной характеристикой, например, такой, как показано на Рис. 1. На диаграмме показан низкоуровневый сигнал f1 с рабочей точкой, установленной для двух положений: Aи B. Отметьте, что выходной уровень fi намного больше в точке В, чем в случае установки в точку А. Теперь взгляните на Рис. 2. На этой диаграмме мы сдвинули рабочую точку, установив её между А и В, вторым высокоуровневым сигналом fo, модулирующим амплитуду сигнала fi. Слово "модулирующий" здесь использовано не в совсем строгом его значении для наглядности, предположим, что сигнал fiявляется несущей, а сигнал fo– модулирующий со звуковой частотой, получаем то, что называется амплитудной модуляцией. Мы наглядно показали, что амплитудная модуляция является таким же процессом, как и смешение, суммарные и разностные компоненты, по отношению к модуляции составляют боковые полосы.

 Следующее наблюдение следует сделать относительно уровней сигналов fi и fo. Сигнал fo имеет больший уровень, следовательно, он больше подвержен образованию гармоник частоты fo, генерируемых вследствие нелинейности характеристики смесителя. Сигнал fi сохраняется достаточно на низком уровне и занимает небольшую часть характеристики, которая, в первом приближении, может рассматриваться как прямая, указывая на то, что уровень гармоник сигнала fiбудет небольшим. Это нормальный способ эксплуатации смесителя приёмника, где fi – входной сигнал, а fo - сигнал местного гетеродина. Величина сигнала на входе поддерживается на небольшом уровне, чтобы минимизировать образование гармоник и интермодуляционных продуктов с другими источниками сигнала и гармониками fi, обусловленными кривизной характеристики смесителя. Обэтом в нижеследующих параграфах.

Мультипликация (перемножение)

Вернёмся к обсуждению Рис. 2, процесс смешения есть математически частный случай перемножения. Действующая амплитуда сигнала fi перемножается на действующую амплитуду сигнала fo, отсюда результирующие компоненты называются продуктами. Всё, конечно, выглядит конфузно, поскольку мы знаем, что получаемые на выходе смесителя частоты равны сумме и разности частот подводимых к смесителю сигналов. Но нужно понимать, что перемножаются только действующие амплитуды, а не частоты, а само явление может быть объяснено одним из хорошо известных тригонометрических тождеств:

sin(A) sin (B) = (1/2) cos(A + B) - (1/2) cos(A - B)        ... (1)

Мы можем выразить действующую амплитуду f1 и foследующим образом:

Ai.sin(2π.fi.t) и Ao.sin(2π.fo.t),

где Aiи Ao- их соответствующие амплитуды и t = время.

Перемножая их с заменой в тождестве (1), мы получаем следующее:

Ai.sin(2π.fi.t).Ao.sin(2π.fo.t)= (1/2)AiAo{cos[2π.t(fo + fi)]- cos[2π.t(fo - fi)]}

Можно видеть, что две новые функции косинуса (fo + fi) и (fo - fi) сформированы для замены суммарной и разностной частот. Конечно же, косинусоида - та же самая синусоида, но сдвинутая по фазе на 90 градусов.

Продукты смешения

На выходе смесителя присутствуют намного больше компонентов, чем просто суммарная и разностная от входных. Чтобы проиллюстрировать это на спектроанализаторе, соберём простую смесительную схему на германиевом диоде (Рис. 3.) Сигнал fo напряжением 1 Врр подан параллельно диоду, что достаточно, чтобы сдвинуть его рабочую точку по кривой вольт-амперной характеристики диода, а сигнал fi имеет уровень менее 0,1 Врр. Выбор частот в 150 и 200 кГц для fi и fo, соответственно, не имеет какого-либо значения, кроме демонстрационного.

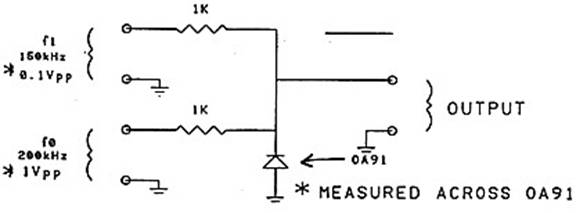
Рис. 3. Простой диодный смеситель

 

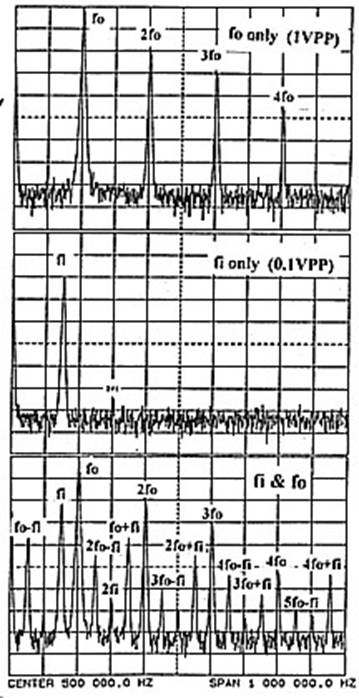
Рис. 4. Частотный спектр простого диодного смесителя
(Напряжения на диоде: fo = 1 Вpp, fi = 0,1 Вpp)
Ось Y - 10 дБ на деление.

Рис. 4 в трёх частях показывает выход смесителя, когда на него поданы сигналы с частотами или foили fi и когда эти сигналы поданы одновременно для смешения. Отметьте высокий уровень гармоник от сигнала fo, по сравнению с сигналом fi. Гармоника 2foсоставляет величину лишь на 20 дБ меньшую, чем fo, тогда как гармоника 2f1 на 45 дБ ниже f1, а более высокие гармоники fi ещё менее заметны. Отметьте также, что на выходе смесителя, при смешении, образуются не только суммарные и разностные частоты от fi и fo, но и суммарные и разностные продукты от fo. (если быть более строгим, то тоже самое образуется и от частоты fi, но уровень этих продуктов намного ниже и зачастую относится к шуму – UA9LAQ).

Если комбинационные продукты нежелательны, то опасность их и степень подавления зависит от того, насколько близко они расположены к требуемой (суммарной или разностной) частоте, отсюда зависит и полоса пропускания фильтра, следующего за смесителем, с помощью которого будет выделяться сигнал необходимой частоты после смешения. Допустим, что мы собрались использовать выходную суммарную компоненту (fo + fi), тогда ближайшие к ней комбинационные частоты более высоких порядков будут: (fo - fi) и 3(fo - fi). Учитывая, что их уровень невысок, они не составят большой проблемы. На что следует обратить внимание, так это на высокий уровень сигнала с частотой fo, проще: сигнала гетеродина, который на 36 дБ выше комбинационной компоненты (fo + fi) - суммарного сигнала ПЧ, и на 2fo, прилегающую к (fo + fi) и имеющую уровень на 16 дБ выше её.

На Рис. 5 показано, что произойдёт, если мы увеличим уровень сигнала fi до уровня fo. Уровни получаемых суммарной и разностной компонент подрастут, как и уровни других продуктов, плюс (теперь уже с заметным уровнем) появятся суммарные и разностные продукты гармоник частоты fi.

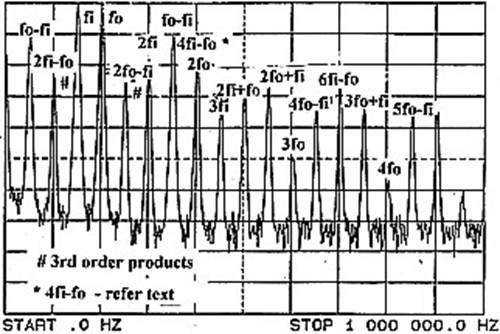
Рис. 5. Простой диодный смеситель
(Напряжения на диоде: fо = 1 Врр, fl = 1 Врр)
Ось Y - 10 дБ на деление.

Из-за конкретно выбранных частот 200 и 150 кГц, выбранных для foandfi, некоторые гармоники и комбинационные сигналы совпадают по частотам (увеличивая наложением амплитуду этих компонент – UA9LAQ), что очевидно из Рис. 5. (Например, 2foи (4fi - fo) совпадают на частоте 400 кГц). Это проиллюстрировано на Рис. 6, где f1 сдвинута вниз к 115 кГц, обнажая ещё много компонентов, включая (4f1 - fo), которая теперь расположится на частоте 260 кГц.

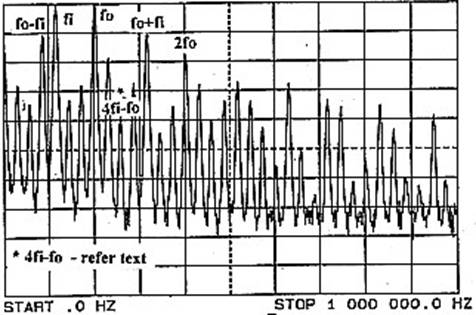
Рис. 6. Простой диодный смеситель.
(Напряжения на диоде: fo = 1 Вpp, fi = 1 Вpp)
fi изменена на 115 кГц
Ось Y– 10 дБ на деление.

Если взять проблему присутствия сигнала foна выходе смесителя с уровнем 35 дБ выше необходимой комбинационной компоненты, например, суммарной: (fo + fi), то можно применить балансный смеситель и нивелировать эту входную компоненту. Для демонстрации этого блок промышленного двухбалансного смесителя типа СМ1 (Рис. 1) был установлен на испытательный стенд, и на него были поданы сигналы с теми же частотами 200 кГц (fo) и 150 кГц (f1). Полученный спектр показан на Рис. 8. Видно, что теперь уровень обоих сигналов и f1 и fo находится ниже уровня комбинационной суммарной компоненты (fo + fi) на 35 дБ. Балансные смесители рассмотрены ниже.

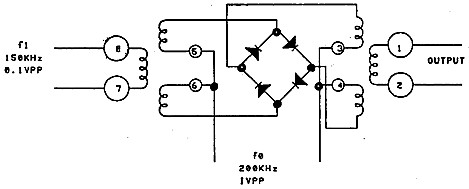
Рис. 7. Двойной балансный кольцевой смеситель типа CM1.

 

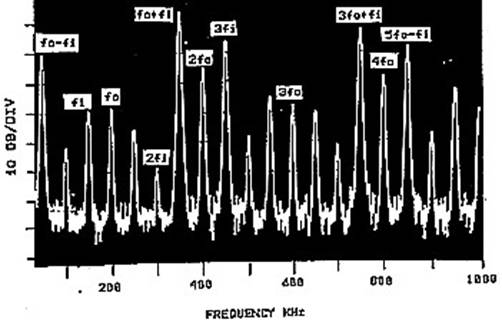
Рис. 8. Частотный спектр двойного балансного смесителя.

Виды смешения

Смесители можно классифицировать на работающие в непрерывном нелинейном режиме (Рис. 2) и ключевые.

Типичным смесителем первого типа является схема на двухзатворном полевом транзисторе, показанная на Рис. 9. У ПТ – квадратичная характеристика, которая с успехом может быть применена для смешения. Из-за высоких входных импедансов ПТ требуют небольшой входной мощности, отдельные затворы обеспечивают хорошую развязку между двумя смешиваемыми сигналами.

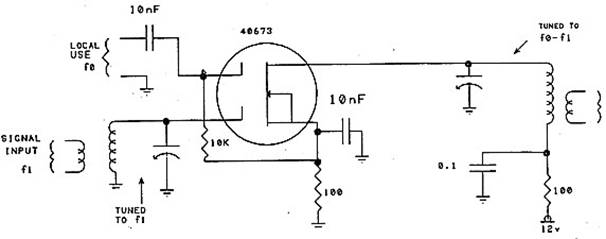
Рис. 9. Смеситель на двухзатворном полевом транзисторе с изолированными затворами в непрерывном нелинейном режиме.

Большинство смесителей на биполярных транзисторах и лампах работают в непрерывном нелинейном режиме. По сравнению с квадратичной характеристикой ПТ, биполярные транзисторы и полупроводниковые диоды имеют экспоненциальные характеристики, а вакуумные лампы подчиняются закону степени 3/2 (Для ясности оставляю предложение из оригинала полностью: By comparison to the square law of the MosFET, the bipolar transistor and the semiconductor diode have an exponential characteristic and the vacuum tube a 3/2 power law. – UA9LAQ).

Квадратичная характеристика ПТ больше приемлема потому, что генерация гармоник, при ней, теоретически, ограничена вторым порядком. Этоможетбытьустановленодругимизвестнымтригонометрическимтождеством:

cos(2A) = 1- 2sin²A и

sin²A = (1/2) (1 + cos(2A))

Отсюда, если возвести в квадрат входную компоненту f, выраженнуюкак Af.sin(2π.f.t), то мы получим:

[Af.sin(2π.f.t)]² = (1/2)Af² [1 + cos(2π.2f.t)]

У нас получится частота - 2f (вторая гармоника), другие отсутствуют. Это также означает, что в нашем квадратичном смесителе продукты высших порядков ограничены третьим порядком: (2fo+fi) и (2fi+fo).

Чтобы сравнить с этим экспоненциальный закон характеристики биполярного транзистора или диода, мы можем продлить экспоненциальную функцию, используя последовательность Тейлора (Taylor series):

e^x = 1 + x + x²/2! + x³/3! + x⁴/4! etc.

Подставим x = sin (2π.f.t) и мы получим следующее:

sin(2π.f.t), sin²(2π.f.t), sin³(2π.f.t), sin⁴(2π.f.t), и в действительности, все мощности, равные sin(2π.f.t).

Мы видели, что синусоидальный, возведённый в квадрат, сигнал даёт вторую гармонику, теперь исследуем компоненту синусоидальный сигнала, возведённого в куб (у кубической характеристики – экспоненциальный вид – UA9LAQ). Для этого используем третье тригонометрическое тождество:

sin(3A) = 3sinA - 4sin².3A

Преобразование формы даст:

sin³A =         (3/4)sinA - (1/4)sin(3A)

Подставляя 2π.f.t = A, получим sin[3(2π.f.t)] , вытекающее из определения куба синусоиды экспоненциальной функции, что подтверждает генерацию третьей гармоники.

Не вдаваясь в другие математические подробности, мы можем предсказать, что складывается закономерность, в которой каждая прибавляемая мощность sin(2π.f.t) даёт соответствующее приращение порядка гармоник. Приняв это за истину, можно сделать вывод, что экспоненциальная характеристика биполярного транзистора или полупроводникового диода, способствует генерации гармоник всех порядков, в сравнении с квадратичной характеристикой ПТ с изолированным затвором, которая способствует появлению только второй гармоники.

Ключевые смесители

Вторыми в классификации рассмотрим ключевые смесители. Эти смесители работают переключением входного сигнала (f1) из одного состояния в другое (включено-выключено) в течение каждого полупериода управляющего сигнала (fo). Рис. 7 показывает двухбалансный ключевой смеситель, в котором диоды служат переключателями. Диоды попарно открываются, в зависимости от полярности прилагаемого к ним напряжения с частотой fo и это переворачивает каждый раз фазу f1. Процесс переключения проиллюстрирован на Рис. 10 и 11: на первом показан случай, когда частота fi выше, чем fo, на втором - fi ниже fo. Сигнал, fi, в действительности перемножается на прямоугольные импульсы с частотой следования fo, с соответствующей амплитудой и даёт следующие основные и гармонические компоненты:

(4/π)[cos(2π.fo.t) - (1/3)cos(2π.3fo.t) + (1/5)cos(2π.5fo.t) ... etc] ----------------(2)

Это означает, что fi перемножается с основной частотой fo и всеми её нечётными гармониками. (Отметьте, что идеальные прямоугольные импульсы не содержат чётных гармоник).

Ситуация упрощается, так как прямоугольные импульсы имеют только два состояния (по амплитуде, и в идеале – UA9LAQ), единица и минус единица (логические уровни – UA9LAQ), так что, чтобы умножить на fi, необходимо перемножить fiи на единицу и на минус единицу, что означает переворот фазы fi, при каждой смене полярности fo.

Смеситель определяется как двухбалансный, поскольку оба входных сигнала сбалансированы (взаимно уничтожены – UA9LAQ) относительно выхода. Подавление уровня входных сигналов предварительно упомянуто и проиллюстрировано на Рис. 8.

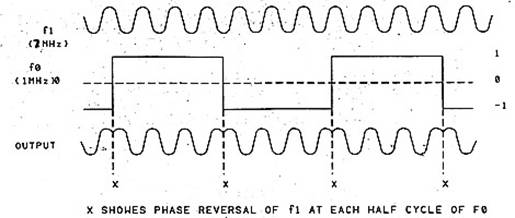
Рис. 10.
Двойной балансный смеситель. Коммутация сигнала с частотой f1 сигналом с частотой fo ( fi выше fo).

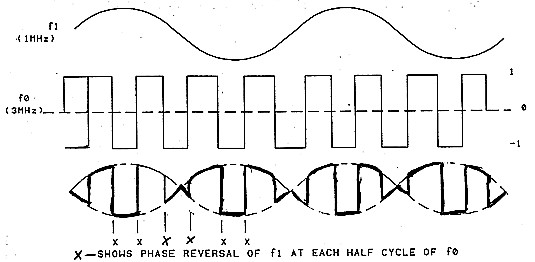
Рис. 11.
Двойной балансный диодный смеситель. Коммутация сигнала с частотой fi сигналом с частотой fo (fiниже fo).

Другим типом диодного ключевого смесителя является однобалансный полукольцевой, показанный на Рис. 12. В этой схеме диоды включаются и выключаются во время противоположных полуволн сигнала (напряжения) частотой fo, как показано на Рис. 13. В этом случае, мы не можем сделать заключение, что сигнал частотой fi ( и амплитудой Ai) перемножается на прямоугольные импульсы с частотой следования fo и с амплитудой в единицу, речь пойдёт о сдвиге по постоянному току с амплитудой в единицу. Однако, перемножаявходныесоставляющие, получимследующийрезультат:

Ai.sin(2π.fi.t).(1 + [последовательность прямоугольных импульсов (2)])

Сдвиг по постоянному току заменён единицей и, умножая это на Ai.sin (2π.fi.t), заменяющее сигнал частотой fi, мы и получим сигнал той же частоты fi, отсюда, fi - не сбалансирован относительно выхода этого смесителя. Напротив, сигнал переключения частотой fo - сбалансирован, а отсюда и название смесителя – однобалансный.

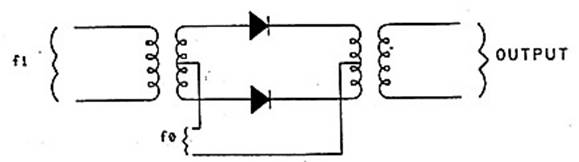
Рис. 12. Однобалансный смеситель (полукольцо).

 

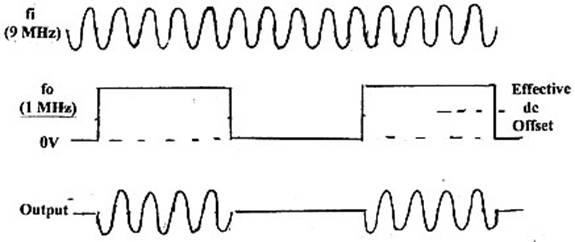
Рис. 13. Однобалансный диодный смеситель.
(fi перемножается переключающим напряжением fo, амплитуда сигнала равна амплитуде переключающего напряжения).

Выход

Степень изоляции входного сигнала в балансном смесителе определяется тщательностью балансировки трансформатора и согласованием диодов. На заре эры полупроводников, некоторые телефонные системы использовали купруксные выпрямители. Современные же сбалансированные смесительные модули, которые подходят и для применения на УКВ и СВЧ, включают в себя быстродействующие диоды, характеризующиеся малым напряжением на них в проводящем состоянии, малым обратным током, малой величиной собственной ёмкости и очень высоким значением максимально применимой частоты.

Диоды всех типов имеют “изогнутую” характеристику включения (начальный участок) и, тем не менее, могут, жёстко управляемые сигналом fo, работать в частично непрерывном нелинейном режиме. В спектре балансного смесителя, показанном на Рис. 8, чётные гармоники fo ясно показывают, что отсутствует идеальное переключение по закону прямоугольных импульсов.

Диодные балансные смесители работают очень хорошо, но обладают скорее потерями преобразования, чем усилением. Они также являются устройствами с низким импедансом и требуют для работы с ними низкого импеданса источника схем “привязанных” к ним. Из-за этих характеристик диодов, часто используются активные смесители на биполярных или полевых транзисторах. Эти смесители имеют усиление при преобразовании и могут работать со схемами “обвязки”, имеющими более высокий импеданс.

Схема активного балансного смесителя, построенного автором для использования в трансивере, показана на Рис. 14. В этом случае, SSB сигнал смешивался с несущей, имеющей частоту 21 МГц для получения ПЧ в 17 МГц (преобразование вверх). Спектр этого смесителя показан на Рис. 15. Этот смеситель работает в непрерывном нелинейном режиме, сигнал fo заставляет напряжение на затворах изменять ток стока в большой части характеристики зависимости тока стока от напряжения на затворе. Точный баланс усилений транзисторов достигается дифференциальной регулировкой (подстройкой) токов стоков потенциометром, регулирующим смещение в цепи истоков.

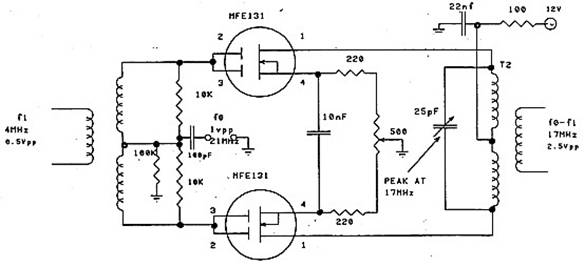
Рис. 14. Балансный смеситель на ПТ.
T1 -10 витков тройным проводом на кольце Рhilips 97120, μ = 2300
T2 - 8 витков тройным проводом на кольце Рhilips 97160, μ = 120

 

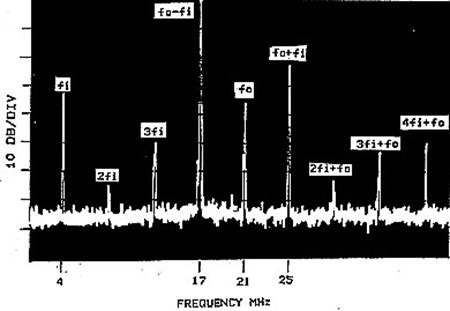
Рис. 15.
Спектральный анализ балансного смесителя на ПТ.

Активные балансные смесители могут работать также в ключевом режиме, в который их можно перевести увеличением уровня сигнала fo до точки, где выходной ток переключается между двумя уровнями: нулевым (выключено) и током насыщения (включено). В каком режиме работать смесителю определяется уровнем напряжения foи в некоторой степени установкой начального смещения входа.

Смешение при преобразовании вверх и вниз

Вы можете задать вопрос: где преимущественно применяется балансный смеситель по отношению к небалансному? Один ответ на вопрос лежит в том, насколько сложно удалить опорную частоту настройкой или фильтрованием. В случае, показанном на Рис. 14, несущая с частотой 21 МГц расположена достаточно близко к выбранной компоненте - частоте ПЧ 17 МГц, и выбрана балансная схема, так как, в противном случае, возникает опасность появления остаточного (опасного) уровня сигнала опорной частоты (частоты гетеродина) в выходном сигнале (ПЧ).

Такое же частотное преобразование, наоборот, требуется, когда 17 МГц преобразуется в ПЧ 4 МГц с использованием напряжения гетеродина той же частоты 21 МГц. В этом случае, однако, частота 21 МГц отстоит далеко от ПЧ 4 МГц и может быть легко отфильтрована, а в качестве смесителя можно использовать обычную схему смесителя на двухзатворном ПТ, показанную на Рис. 9.

Следует сделать особое ударение на том, что балансный смеситель желателен во всех случаях с преобразованием вверх, как это обычно делается в SSB передатчиках, преобразование вниз, которое встречается большей частью в приёмниках, менее критично к этому требованию. Другим примером применения балансного смесителя является амплитудный модулятор, который даёт на выходе двухполосный сигнал с подавленной несущей. Сигнал f1 является здесь звуковым (от микрофонного усилителя), а сигнал несущей (опорной частоты) fo балансируется (подавляется). В этом случае, смеситель обычно называется балансным модулятором. Вспомните, мы уже упоминали ранее, что смешение и амплитудная модуляция являются одним и тем же процессом. Балансный модулятор является первым каскадом в SSB – передатчике, где получаются две боковые полосы сигнала, одна из которых позднее удаляется избирательным фильтром.

Продукты интермодуляции

Поскольку наше смесительное устройство работает в нелинейном режиме для выполнения функции смесителя, то оно генерирует и интермодуляционные продукты от нежелательных сигналов, попадающих на его вход. Продукты могут возникать как результат смешения нашего сигнала fi (который мы теперь будем называть f1) с другим сигналом f2 или в результате смешения совершенно разных сигналов f2 и f3. Наиболее “беспокоящими” являются для нас, так называемые, продукты третьего порядка (2f1-f2) или (2f2 - f1). Они наиболее опасны потому, что являются ближайшими по частоте продуктами интермодуляции к f1.

Примем частоту требуемого сигнала f1 равной 14,200 МГц, а другой сигнал f2 имеет частоту 14,300 МГц. В этом случае, продукты третьего порядка будут иметь частоты 14,100 и 14,400 МГц. Предположим также, что имеется и третий сигнал С на частоте 14,400 МГц и вычислим продукты интермодуляции третьего порядка от f2 и f3, т. е., (2f2 - f3) и (2f3 - f2). Из этого мы получим 14,200 и 14,500 МГц, первое значение совпадает с частотой необходимого принимаемого сигнала f1, что явится причиной помехи.

Интерференционные помехи могут составлять серьёзную проблему и поэтому одним из параметров смесителя является уровень его продуктов третьего порядка на выходе относительно уровня необходимой суммарной или разностной компоненты.

Точка пересечения по продуктам интермодуляции третьего порядка

Выше было упомянуто, что для уменьшения уровня интермодуляционных составляющих, необходимо иметь входной сигнал fiна низком уровне. Исследуем это утверждение:

Предположим, что мы подвели два синусоидальных сигнала с одинаковой амплитудой ко входу нелинейного устройства. Заметим уровни и увеличим их в 3,16 раза (или на 10 дБ). Из-за нелинейности увеличение на выходе будет не таким, как на входе, однако, выходной спектр может быть пересчитан в компоненты, состоящие из двух основных частот f1 andf2, и другие компоненты, которые можно анализировать отдельно. Сигналы основных частот должны возрастать линейно, иначе, они не будут основными, отсюда их выходные напряжения должны возрастать на строго предложенную относительно входа величину (т. е., 3.16). Другие компоненты будут описаны иными уравнениями.

Ранее мы обращались к тригонометрическому тождеству: cos(2A) - 1/2(sin**2A) и показывали, что компоненты второй гармоники ассоциируются с функцией квадрата синусоиды, отсюда мы можем сделать вывод, что компоненты второй гармоники 2f1 и 2f2 следуют функции квадрата входного уровня. Конечно же, в нашем случае, нам более интересен уровень продуктов третьего порядка, результаты перемножения 2f2 на f1 и 2f1 на f2. При fiи f2, одинаковых по амплитуде, результат будет таковым, что продукты третьего порядка (2f2 - f1) и (2f1 - f2) будут следовать кубической зависимости относительно входных уровней. Если свести наше изменение в 3,16 раза в таблицу в децибельном виде, то мы получим следующее:

Изменение входного уровня - 20 LOG 3.16 - 10 dB

Изменение выходного уровня основных частот - 20 log 3.16 = 10 dB

Изменение выходного уровня продуктов третьего порядка = 20 log 3.16**3 = 30 dB

(Знаки привожу как в оригинале – UA9LAQ).

Поскольку интермодуляционные продукты возрастают по кубическому закону изменения входных уровней, в противоположность линейному для основных сигналов, то чем выше уровень входных сигналов, тем больше будет соотношение между уровнем продуктов интермодуляции и основных сигналов. Теоретически существует точка, где уровень продуктов интермодуляции сравняется с выходным уровнем основных сигналов. Эта точка называется точкой пересечения по продуктам интермодуляции третьего порядка и часто приводится в характеристиках на смесители.

Чтобы измерить эту точку, соберём стенд, показанный на Рис. 16. Два калиброванных сигнал-генератора с одинаковым уровнем сигнала подключены ко входам смесителя, на вход смесителя подключен калиброванный спектроанализатор. Поскольку устройство – смеситель, то и основные и продукты третьего порядка сдвинуты по частоте на значение (частоту гетеродина). В случае, на Рис. 16, действующие выходные компоненты: необходимый сигнал ПЧ (fo - f1) и компоненты третьего порядка [fo - (2f1 - f2)] и [fo - (2f2 - f1)]

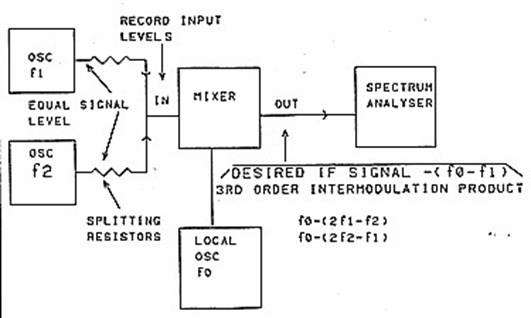
Рис. 16.
Испытательный стенд для исследования смесителей.

 

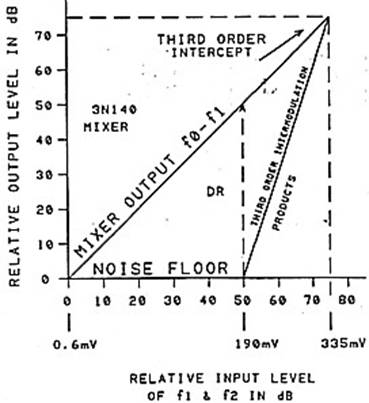
Рис. 17. Характеристика работы смесителя на 3N140. Показана точка пересечения по продуктам интермодуляции третьего порядка.
DR = динамический диапазон по уровню неразличимых продуктов интермодуляции.

На Рис. 17 показаны кривые смесителя на 3N140, вытекающие из исследования с Рис. 16. Чтобы выполнить его, пришлось входные уровни установить таковыми, что продукты интермодуляции третьего порядка сравнялись с уровнем шумов. Анализатор спектра использовался для того, чтобы отделить различные компоненты визуально друг от друга и измерить их уровни. Всё что нужно учесть, так это уровни входных и выходных необходимых сигналов и уровень интермодуляционных продуктов. Довольно просто продолжить кривые, основанные на линейной и кубической зависимости (до пересечения). В децибельной форме формируется две линии с разным наклоном. Нужный сигнал возрастает на выходе на 10 дБ, при увеличении входного на 10 дБ. Интермодуляционные продукты (IMD) третьего порядка возрастают на 30 дБ при увеличении на 10 дБ по входу. Для подтверждения результатов исследования можно несколько раз повторить опыт с различными уровнями сигналов.

В некоторой точке линии сойдутся, обозначая точку пересечения по интермодуляции третьего порядка. Следует особо отметить, что эта точка – теоретическая и никогда не может быть достигнута на практике, поскольку смеситель войдёт в режим компрессии сигнала раньше, чем эта точка будет достигнута. Определение этой точки полезно, поскольку обе характеристики и линейная и кубическая могут быть восстановлены с помощью соответствующих закономерностей: линейной и кубической зависимости.

Уровень шума и динамический диапазон

Используя аппаратуру с Рис. 16, можно установить другой важный параметр смесителя, - уровень шумового порога на его выходе. Как было упомянуто выше, чем меньше уровень входного сигнала, тем меньше уровень продуктов интермодуляции. Однако, чем меньше уровень входного сигнала, тем меньше и соотношение сигнал/шум. (Вот те “ножницы”, которые ограничивают динамический диапазон смесителя: снизу - шум, сверху – интермодуляция – UA9LAQ).

На Рис. 17 уровень шума обозначен как 0 дБ на выходе и эта информация, вместе с уровнями сигнала и интермодуляционных продуктов, переведена в другую форму, представленную наРис. 18. Здесь мы показываем отношение сигнал/шум, как функцию от уровня входного сигнала на одной кривой, а отношение уровня сигнала к уровню продуктов интермодуляции как функцию входного сигнала – на другой. Отметьте, что здесь имеется оптимальный уровень, там, где пересекаются кривые, и, где уровень выходного сигнала на 50 дБ выше как уровня шумов, так и продуктов интермодуляции.

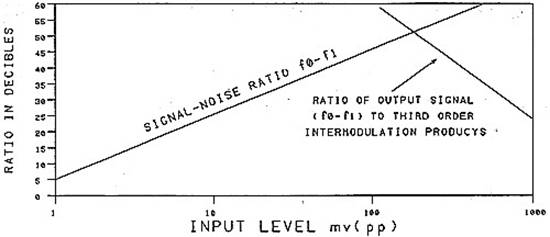
Рис. 18. Смеситель на 3N140.
Сравнение сигнал/шум и сигнал/продукты интермодуляции.

Для уровней сигналов ниже точки пересечения IMD продукты находятся ниже шумового порога. Это показано также пунктирной линией на Рис. 17.Длина этой линии является также динамическим диапазоном (DR) смесителя, при котором мы не обнаруживаем продуктов интермодуляции. Отметьте, что эта цифра составляет 50 дБ и две трети разности между точкой пересечения по продуктам интермодуляции третьего порядка и шумовым порогом (75 дБ). По линейному и кубическому законам двух кривых, соответственно, динамический диапазон (в дБ) может быть всегда определён как 2/3 между точкой пересечения и порогом шума.

Высокий динамический диапазон бесспорно важен, когда смеситель используется в супергетеродинном приёмнике, который имеет дело с большим разбросом уровней входных сигналов. Для удовлетворительной работы, самый малый сигнал должен быть усилен РЧ усилителем до уровня, превышающего уровень шума смесителя, но не слишком сильно, чтобы избежать появления продуктов интермодуляции под действием сильных сигналов. При этом, максимальный уровень нежелательных сигналов также должен находиться в пределах динамического диапазона приёмника. Если это не так, - ждите появления интермодуляционных продуктов. Для больших уровней сигналов необходимо обеспечить меньшее усиление сигналов в УРЧ, применить регулировку усиления по РЧ (или (и) обеспечить приёмник аттенюатором на входе – UA9LAQ).

Другим фактором, который следует упомянуть, является также тот, что уровень шума зависит от полосы пропускания: пропорционален ей, отсюда: уровень шумового порога и динамический диапазон являются также функциями полосы пропускания системы. Относительно Рис. 17 и 18, измерения были выполнены на базе ЧМ полосы пропускания равной 15 кГц. Если бы полоса пропускания была 3 кГц – SSB, то уровень шумового порога был бы на 7 дБ ниже, а динамический диапазон на столько же бы подрос.

Итоги

Смесители можно классифицировать следующим образом:

1. Работающие в непрерывном нелинейном режиме, или работающие в ключевом режиме.

2. Несбалансированные или сбалансированные, в которых один или оба входных сигнала сбалансированы относительно выхода (подавлены и не присутствуют на выходе смесителя – UA9LAQ).

3. Смесители, которые имеют усиление при преобразовании и смесители, которые имеют при преобразовании потери.

Смесители, обычно, работают при смещении рабочей точки путём опорного сигнала fo по всему нелинейному участку характеристики смесителя, при низком уровне входного сигнала f1, достаточном, чтобы, с одной стороны, обеспечить низкий уровень шума, с другой – минимизировать продукты интермодуляции.

Уровень продуктов смешения третьего порядка возрастает в пропорции к кубу уровня входного сигнала (и выходного). Работу смесителя как функцию уровня входного сигнала можно определить точкой пересечения по продуктам интермодуляции третьего порядка и уровнем шумового порога.

То, что представлено в настоящей статье, является исследованием работы смесителей и изложением некоторых идей по поводу, как нужно их эксплуатировать. Дальнейшую информацию по практическому применению этих устройств можно найти в справочниках, например, публикуемых ARRL (AmericanRadioRelayLeague).

Свободный перевод с английского с разрешения автора: Виктор Беседин (UA9LAQ) ua9laq@mail.ru г. Тюмень март, 2005 г

<< Назад

HOME